Evolutionary dynamics of hawk-dove style games
In this page we explore the evolutionary dynamics of various 'hawk-dove' style games. This game is represented by a fitness payoff matrix of the following form which gives the payoff of each strategy:
| Competitor | ||||||||||
| Focal |
|
The above payoff matrix can be conceptualized as the outcome of competitive interactions for resources (e.g., in a competitive face-off between a hawk and a dove, the hawk gets 2 units of resource and the dove gets none); but the evolutionary dynamics are analyzed by modeling these interaction payoffs as relative fitnesses. Note that the matrix is scale independent - that is, the evolutionary dynamics depend only on the ratio of different elements in the matrix, not on their scale.
Each result is given by a two panel graph. The upper panel shows changes in the relative frequencies of each strategy through time. The lower panel shows the mean fitness of the population over the same period. So, for instance, here is the result using the payoff matrix given above for 50 generations with an initial frequencey of f(hawk)=0.01 and f(dove)=0.99:
Figure 1.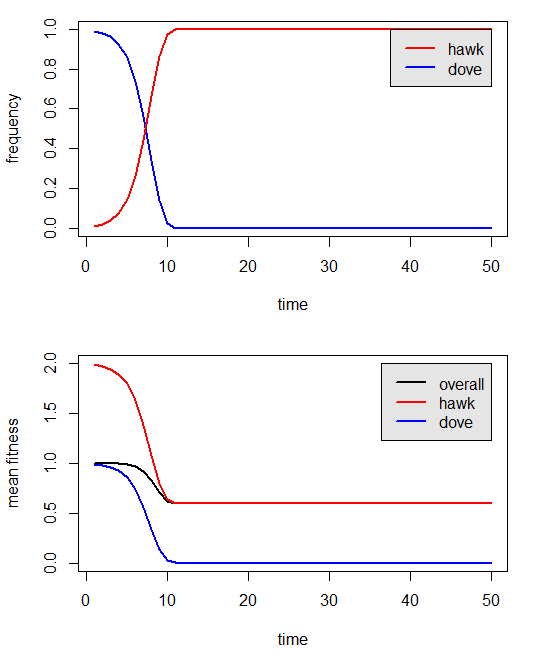
The result in Figure 1 can be interpreted as follows: the hawk strategy is highly fit when rare. It goes to fixation, which suggests that the hawk strategy is also evolutionarily stable (an ESS). The population mean fitness is highest at the start of the simulation, as is the mean fitness of each strategy (i.e., hawks are fittest when rare); however mean fitness declines through time to an equilibrium level of 0.6. The fitness of the dove strategy approaches zero when doves are rare, suggesting that the dove strategy is not evolutionarily stable under this model parameterization.
Now let's consider different values for the payoff matrix:
| Competitor | ||||||||||
| Focal |
|
Here, doves receive some payoff even in encounters with hawks. (Perhaps, for example, hawk aggression is traded-off against an ability to find food. Doves find food resources more efficiently and are able to eat before hawks arrive.) Does this modified payoff matrix protect doves against extinction?
Figure 2.
The dove strategy still goes extinct, but the time to extinction is much longer. Let's try a payoff matrix in which the costs of aggression between hawks is further increased, say to 60% of the resource value (such that the fitness of a hawk in a hawk-hawk interaction is 0.4). This corresponds to the following payoff matrix:
| Competitor | ||||||||||
| Focal |
|
And these evolutionary dynamics:
Figure 3.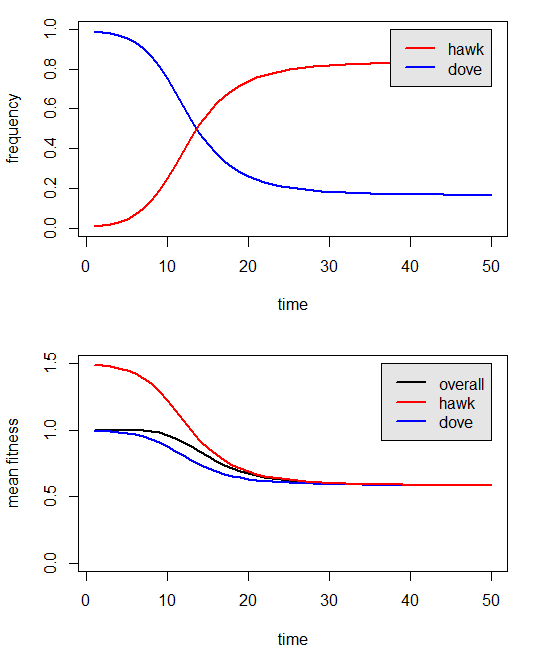
Finally, we have found a model parameterization that suggests coexistence. But perhaps we just have not run our analyses for long enough.... Let's try increasing the number of generations analyzed:
Figure 4.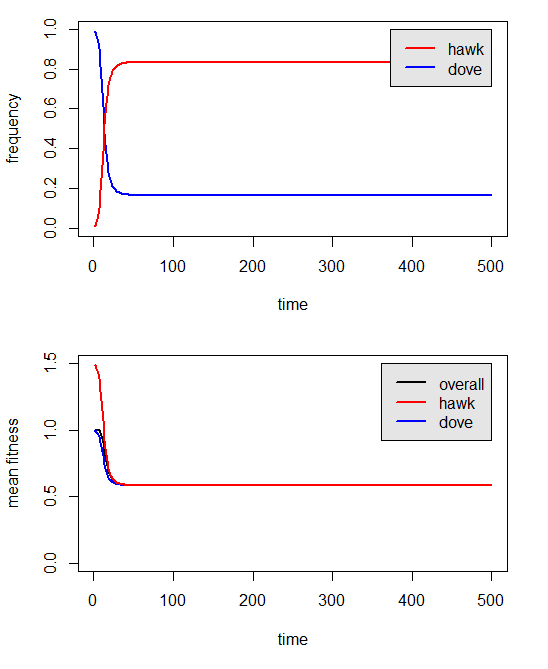
Indeed, hawks and doves can coexist under this payoff matrix. If we start our simulation with a population consisting predominantly of hawks, instead of doves, the same equilibrium frequencies of hawk and dove strategies are reached:
Figure 5.
Without the advantage of computer-based numerical analyses, how can we predict from the payoff matrix whether or not hawks and doves can stably coexist? What's key is the fitness of each strategy when rare. For example, in our first payoff matrix when hawks are rare, they will nearly always encounter doves - resulting a very large fitness advantage for hawks (2:1) when hawks are rare. When doves are rare they will almost invariable pay a significant fitness penalty (0:0.6) when they are rare under that model.
This result contrasts with our final "coexistence" model. Under that parameterization, the fitness payoff to hawks when rare is still quite large (1.5:1); however the fitness disadvantage to doves when rare has actually turned into a slight fitness advantage (0.5:0.4), thus protecting the dove strategy from extinction.
To try these analyses on your own, download the R package 'popgen' from my programs page. Good luck!