Statistical Thinking
If you understand the simple chain of thinking below, you can enlist or hire a statistician who will use the appropriate recipe for the data you have.
1. There is a population of individuals (or entities). (Population = individuals subject to the same foreground causes of interest. There may also be background, non-manipulable causes that vary among these individuals.)
2. For some measurable attribute (e.g., height, income, test score) the individuals have responses to the foreground causes that vary (possibly because of the background causes).
3. You have observations of the measurable attribute for individuals in two or more subsets (samples) of the population.
4. Central question of statistical analysis: Are the subsets sufficiently different in their varying responses that you doubt that they are from the one population (that is, you doubt that they are subject to all the same foreground causes)? Statisticians answer this question with recipes that are variants of a comparison between the averages for the subsets in relation to the spread around the averages. Such a comparison might well lead you to doubt that subsets A and B are from the same population in the left hand situation below, but not in the right hand situation.
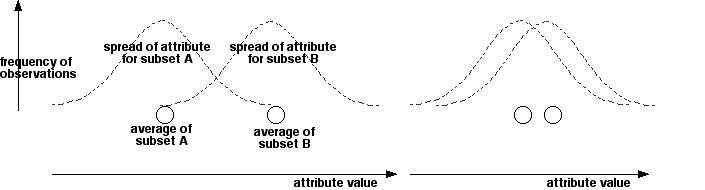
The central question of statistical analysis: Are the averages far apart relative to the spread or not? (left hand versus right hand pictures)
5. If you doubt that the subsets are from the same population, you investigate further, drawing on other knowledge about the subsets. You hope to expose the causes involved and then take action informed by that knowledge about the causes.