Pitágoras (580-500 a. de C.)
Números romanos
|
|
|
|
|
La figura de Pitágoras está envuelta en un halo de leyenda, misticismo y hasta de culto religioso. Y no es tan extraño si pensamos que fue contemporáneo de Buda, de Confucio y de Lao-Tse (los fundadores de las principales religiones orientales)
El término "matemática", al igual que el de filosofía, se le debemos a él.
¿Cuáles
son las principales aportaciones matemáticas de la escuela
pitagórica?...
La
primera y quizás la más importante el introducir la necesidad
de demostrar las proposiciones matemáticas de manera inmaterial
e intelectual, al margen de su sentido práctico. Los pitagóricos
dividieron el saber científico en cuatro ramas: la aritmética
o ciencia de los números - su lema era "todo es número" -,
la geometría, la música y la astronomía.

Armonía musical
Pitágoras descubrió que existía una estrecha relación entre la armonía musical y la armonía de los números.
Si
pulsamos una cuerda tirante obtenemos una nota. Cuando la longitud de la
cuerda se reduce a la mitad, es decir en relación 1:2 obtenemos
una octava.
Si
la longitud era 3:4 obtenemos la cuarta y si es 2:3 tenemos la quinta.

Teorema
de Pitágoras ( Elementos de Euclides)
Pero lo que colmó de gozo a Pitágoras, hasta el punto de mandar sacrificar un buey a los dioses, fue la demostración del famoso teorema. Por desgracia, el secreto que imponía las normas de la sociedad ha hecho imposible que esta demostración llegue a nuestro conocimiento, aunque podemos deducir que no sería muy distinta de la que Euclides nos brinda en sus Elementos.
Sin
duda es el teorema que cuenta con más número de demostraciones.
Scott
Loomis reunió y publicó a principios de este siglo 367 demostraciones.

Hipsicles de Alejandría ( S.II a. de C.) va a proporcionar la definición de número poligonal de d lados y orden n de una forma que algebraicamente equivale a nuestra fórmula
N
(n,d) = n+ 1/2 n ( n -1) ( d -2 )

Son aquellos que verifican que la suma los divisores de uno de ellos coincide con el otro




Edición griega
de los Elementos
Euclides
en el libro más famoso de la Historia de las Matemáticas
recoge gran parte de los conocimientos Pitagóricos sobre los números
y define los números primos y compuestos de forma geométrica:
un número entero es compuesto cuando tiene divisores distintos de
él mismo y de la unidad, es decir cuando se puede dibujar como un
rectángulo numérico.
En el libro IX de los Elementos Euclides nos deja perplejos con su proposición 36, que proporciona un método original para encontrar números perfectos.

"Si tantos números
como se quiera a partir de una unidad se disponen en proporción
duplicada hasta que su total resulte primo, y el total multiplicado por
el último produce algún número, el producto será
perfecto"
Es decir: "Si la suma de las n primeras potencias de 2 es un número primo, entonces el producto de la suma por la última potencia sumada es un número perfecto".
Si
(1+2+22+...+2n) es primo,
entonces
(1+2+22+...+2n)·2n es perfecto
Nicómaco de Gerasa en su Introductio Arithmeticae incluye los 4 primeros números perfectos: 6, 28, 496, 8128
13 = 1; 23 = 3+5; 33 = 7+9+11; ...
Es decir, ya en el siglo I encontramos la solución a uno de nuestros problemas:





El tornillo de Arquímedes

Los espejos ardientes

Sobre la Esfera y el
Cilindro. Museo Vaticano

Muerte de Arquímedes
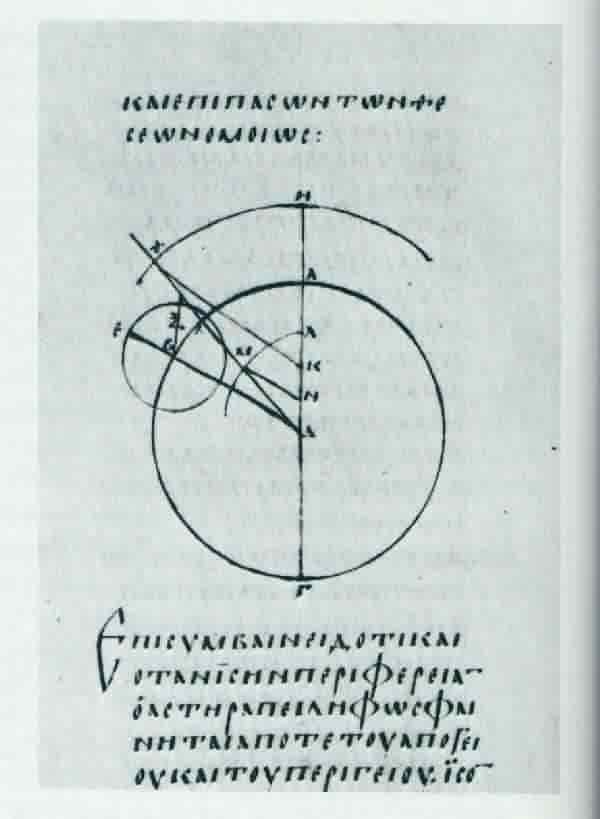
Epiciclos y Deferentes
La Aritmética constaba de 13 libros de los cuales sólo seis sobrevivieron a la destrucción de la gran biblioteca de Alejandría, primero por los cristianos y luego por los musulmanes. En él Diofanto propone más de cien problemas numéricos y da brillantes soluciones a todos ellos.
En 1621 aparece en Francia una traducción al latín de estos seis libros, realizada por Bachet.

Aritmética con las anotaciones de Fermat
El sistema de numeración romano, esas cifras que aún hoy vemos en muchos de nuestros monumentos, no es una buena herramienta para el cálculo.
Utiliza letras del alfabeto para representar los números y no es posicional, es decir cada símbolo vale siempre lo mismo, no importa dónde esté colocado.
Las cifras que utilizaban son éstas: I, V, X, L, C, D, M
El sistema se basa en la suma de los símbolos. Salvo en el caso en que un signo numérico menor preceda a uno mayor:
Por ejemplo: 1336 se escribe MCCCXXXVI
Pero
2894 es: MMDCCCXCIV
