Platonic Solids and Plato's Theory of Everything
The Socratic tradition was not particularly congenial to mathematics
(as may be gathered from A More Immortal Atlas), but it seems that
Plato gained an appreciation for mathematics after a series of
conversations with his friend Archytas in 388 BC. One of the things
that most caught Plato's imagination was the existence and uniqueness
of what are now called the five "Platonic solids". It's uncertain who
first described all five of these shapes - it may have been the early
Pythagoreans - but some sources (including Euclid) indicate that
Theaetetus (another friend of Plato's) wrote the first complete account
of the five regular solids. Presumably this formed the basis of the
constructions of the Platonic solids that constitute the concluding
Book XIII of Euclid's Elements.
In any case, Plato was mightily impressed by these five definite shapes
that constitute the only perfectly symmetrical arrangements of a set
of (non-planar) points in space, and late in life he expounded a
complete "theory of everything" (in the treatise called Timaeus) based
explicitly on these five solids. Interestingly, almost 2000 years
later, Johannes Kepler was similarly fascinated by these five shapes,
and developed his own cosmology from them.
To achieve perfect symmetry between the vertices, it's clear that
each face of a regular polyhedron must be a regular polygon, and all
the faces must be identical. So, Theaetetus first considered what
solids could be constructed with only equilateral triangle faces. If
only two triangles meet at a vertex, they must obviously be co-planar,
so to make a solid we must have at least three triangles meeting at
each vertex. Obviously when we have arranged three equilateral
triangles in this way, their bases form another equilateral triangle,
so we have a completely symmetrical solid figure with four faces,
called the tetrahedron, illustrated below.
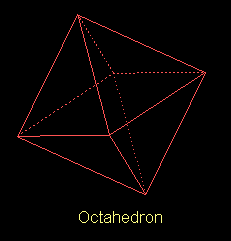
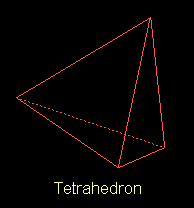 On the other hand, if we make FOUR triangles maeet at a vertex, we
produce a square-bottomed pyramid, and we can obviously put two of
these together, base to base, to give a completely symmetrical
arrangement of eight triangular faces, called the octahedron, shown
below.
On the other hand, if we make FOUR triangles maeet at a vertex, we
produce a square-bottomed pyramid, and we can obviously put two of
these together, base to base, to give a completely symmetrical
arrangement of eight triangular faces, called the octahedron, shown
below.
 Next, we can make FIVE equilateral triangles meet at a point. It's
less obvious in this case, but if we continnue this pattern, adding
equilateral triangles so that five meet at each vertex, we arrive
as a complete solid with 20 triangular faces. This is called the
icosahedron, shown below.
Next, we can make FIVE equilateral triangles meet at a point. It's
less obvious in this case, but if we continnue this pattern, adding
equilateral triangles so that five meet at each vertex, we arrive
as a complete solid with 20 triangular faces. This is called the
icosahedron, shown below.
 Now, we might try putting SIX equilateral triangles together at a
point, but the result is a planar arrangement of triangles, so it
doesn't give a finite solid. I suppose we could regard this as
a Platonic solid with an infinite radius, which might have been
useful in Plato's cosmology, but it doesn't seem to have been viewed
this way. Perhaps this is not surprising, considering the well-known
aversion of the ancient Greek mathematicians to the complete infinity.
In any case, we clearly can't construct any more perfectly symmetrical
solids with equilateral triangle faces, so we must turn to other
possible face shapes.
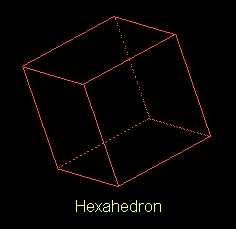
The next regular polygon shape is the square, and again we find that
putting just two squares together does not yield a solid angle, so
we need at least three squares to meet at each vertex. Putting three
squares together we see that we can add three more to give the perfect
solid with six faces, called the hexahedron (also known as the cube).
This is shown below.
Now, we might try putting SIX equilateral triangles together at a
point, but the result is a planar arrangement of triangles, so it
doesn't give a finite solid. I suppose we could regard this as
a Platonic solid with an infinite radius, which might have been
useful in Plato's cosmology, but it doesn't seem to have been viewed
this way. Perhaps this is not surprising, considering the well-known
aversion of the ancient Greek mathematicians to the complete infinity.
In any case, we clearly can't construct any more perfectly symmetrical
solids with equilateral triangle faces, so we must turn to other
possible face shapes.
The next regular polygon shape is the square, and again we find that
putting just two squares together does not yield a solid angle, so
we need at least three squares to meet at each vertex. Putting three
squares together we see that we can add three more to give the perfect
solid with six faces, called the hexahedron (also known as the cube).
This is shown below.
 If we try to make FOUR square faces meet at each vertex, we have
another plane surface (giving another "infinite Platonic solid"), so
clearly this is the only finite perfectly symmetrical solid with
square faces.
Proceding to pentagonal (five-sided) faces, we find that if we put
together 12 pentagons so that three meet at each vertex, we arrive
at the fifth Platonic solid, called the dodecahedron, illustrated
below.
If we try to make FOUR square faces meet at each vertex, we have
another plane surface (giving another "infinite Platonic solid"), so
clearly this is the only finite perfectly symmetrical solid with
square faces.
Proceding to pentagonal (five-sided) faces, we find that if we put
together 12 pentagons so that three meet at each vertex, we arrive
at the fifth Platonic solid, called the dodecahedron, illustrated
below.
 It isn't self-evident that 12 identical regular pentagons would come
together perfectly like this to form a closed solid, but it works,
as Theaetetus proved and as Euclid demonstrates at the conclusion
of The Elements. Of course, if we accept that the icoshedron works,
then the dodecahedron automatically follows, because these two shapes
are "duals" of each other. This means that the icosahedron has 20
faces and 12 vertices, whereas the dodecahedron has 12 faces and 20
vertices, and the angular positions of the faces of one match up with
the positions of the vertices of the other. Thus, once we have the
icosahedron, we can just put a dot in the center of each face, connect
the dots, and viola!, we have a dodecahedron. Similarly, the cube
and the octahedron are duals of each other. Also, the tetrahedron is
the dual of itself (so to speak).
Clearly it's impossible for four (or more) pentagonal faces to meet at
a vertex, because they subtend more than 360 degrees. For hexagonal
(six-sided) faces, three hexagons meeting at a point constitute another
"infinite solid", i.e., so planar surface. It's also obvious that no
higher-order polygon can yield solid, so the five solids already
mentioned (tetrahedron, hexahedron, octahedron, icosahedron, and
dodecahedron) are the only regular polyhedrons.
Theaetetus not only proved that these solids exist, and that they are
the only perfectly symmetrical solids, he also gave the actual ratios
of the edge lengths E to the diameters D of the circumscribing spheres
for each of these solids. This is summarized in Propositions 13
through 17 of Euclid's Elements.
solid E/D
----------- --------------------
tetrahedron sqrt(2/3) 0.81649...
octahedron sqrt(1/2) 0.70710...
hexahedron sqrt(1/3) 0.57735...
icosahedron sqrt[(5-sqrt(5))/10] 0.52573...
dodecahedron [sqrt(5)-1]/[2sqrt(3)] 0.35682...
In Timaeus, Plato actually chose to constitute each of these solids
from right triangles, which played the role of the "sub-atomic
paticles" in his theory of everything. In turn, these trianglular
particles consisted of the three legs (which we might liken to quarks),
but these legs were ordinarily never separated. The right triangles
that he chose as his basis particles were of two types. One is
the "1,1,sqrt(2)" isoceles triangle formed by cutting a square in
half, and the the other is the "1,2,sqrt(3)" triangle formed by
cutting an equilateral triangle in half. He used these to construct
the faces of the first four solids, but oddly enough he didn't just
put two together, he used six "1,2,sqrt(3) triangles to make a
triangular face, and four "1,1,sqrt(2)" triangles to make a square
face, as shown below.
It isn't self-evident that 12 identical regular pentagons would come
together perfectly like this to form a closed solid, but it works,
as Theaetetus proved and as Euclid demonstrates at the conclusion
of The Elements. Of course, if we accept that the icoshedron works,
then the dodecahedron automatically follows, because these two shapes
are "duals" of each other. This means that the icosahedron has 20
faces and 12 vertices, whereas the dodecahedron has 12 faces and 20
vertices, and the angular positions of the faces of one match up with
the positions of the vertices of the other. Thus, once we have the
icosahedron, we can just put a dot in the center of each face, connect
the dots, and viola!, we have a dodecahedron. Similarly, the cube
and the octahedron are duals of each other. Also, the tetrahedron is
the dual of itself (so to speak).
Clearly it's impossible for four (or more) pentagonal faces to meet at
a vertex, because they subtend more than 360 degrees. For hexagonal
(six-sided) faces, three hexagons meeting at a point constitute another
"infinite solid", i.e., so planar surface. It's also obvious that no
higher-order polygon can yield solid, so the five solids already
mentioned (tetrahedron, hexahedron, octahedron, icosahedron, and
dodecahedron) are the only regular polyhedrons.
Theaetetus not only proved that these solids exist, and that they are
the only perfectly symmetrical solids, he also gave the actual ratios
of the edge lengths E to the diameters D of the circumscribing spheres
for each of these solids. This is summarized in Propositions 13
through 17 of Euclid's Elements.
solid E/D
----------- --------------------
tetrahedron sqrt(2/3) 0.81649...
octahedron sqrt(1/2) 0.70710...
hexahedron sqrt(1/3) 0.57735...
icosahedron sqrt[(5-sqrt(5))/10] 0.52573...
dodecahedron [sqrt(5)-1]/[2sqrt(3)] 0.35682...
In Timaeus, Plato actually chose to constitute each of these solids
from right triangles, which played the role of the "sub-atomic
paticles" in his theory of everything. In turn, these trianglular
particles consisted of the three legs (which we might liken to quarks),
but these legs were ordinarily never separated. The right triangles
that he chose as his basis particles were of two types. One is
the "1,1,sqrt(2)" isoceles triangle formed by cutting a square in
half, and the the other is the "1,2,sqrt(3)" triangle formed by
cutting an equilateral triangle in half. He used these to construct
the faces of the first four solids, but oddly enough he didn't just
put two together, he used six "1,2,sqrt(3) triangles to make a
triangular face, and four "1,1,sqrt(2)" triangles to make a square
face, as shown below.
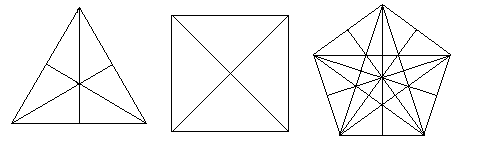 Of course, it's not possible to build a pentagon from these two
basic kinds of right triangles, and Plato doesn't actually elaborate
on how the faces of the dodecahedron are to be constructed, but from
other sources we know that he thought each face should be comprosed
of 30 right triangles, probably as shown on the right-hand figure
above, so that the dodecahedron consisted of 360 triangles. The
tetrahedron, octahedron, and icosahedron consisted of 24, 48, and
120 triangles (of the type 1,2,sqrt(3)), respectively, and the
hexahedron consisted of 24 triangles (of the type 1,1,sqrt(2)).
Now, if the basic triangles were the subatomic particles, Plato
regarded the solids as the "atoms" or corpuscles of the various
forms of substance. In particular, he made the following
identifications
number of triangles
type 1 type 2
------ ------
tetrahedron = plasma ("fire") 24 0
octahedron = gas ("air") 48 0
icosahedron = liquid ("water") 120 0
hexahedron = solid ("earth") 0 24
The idea that all the constituients of nature consist of mixtures of a
small number of "elements", and in particular the selection of the four
elements of earth, water, air, and fire, is attributed to an earlier
Greek philosopher Empedocles of Agrigentum (495-435 BC). Empedocles
believed that although these elements (which he called "the roots of all
things") could be mixed together in various proportions, the elements
themselves were inviolable, and could never be changed. In contrast, one
of the intriguing aspects of Plato's theory was that he believed it was
possible for the subatomic particles to split up and re-combine into other
kinds of atoms. For example, he believed that a corpuscle of liquid,
consisting of 120 "type 1" triangles, could be broken up into five
corpuscles of plasma, or into two corpuscles of gas and and one of plasma.
Also, he believed that the "smaller" corpuscles could merge into larger
corpuscles, so that (for example) two atoms of plasma could merge and form
a single atom of gas. However, since the basic triangles making up "earth"
(cubes) are dis-similar to those of the other forms of substance, he held
that the triangles comprising cubes cannot be combined into any of the
other shapes. If a particle of earth happened to be broken up into its
constituient triangles, they will "drift about - whether the breaking
up within fire itself, or within a mass of air or water - until its
parts meet again somewhere, refit themselves together and become earth
again".
When Plato asserts that the [1,1,sqrt(2)] triangles cannot combine
into anything other than a cube, it's conceivable that he was basing
this on something more that just the geometric dis-similarity between
this triangle and the [1,2,sqrt(3)] triangle. He might also have
had in mind some notion of the incommensurability of the magnitudes
sqrt(2) and sqrt(3), not only with the unit 1, but with each other.
Indeed the same Theaetetus who gave the first complete account of the
five "Platonic" solids is also remembered for recognizing the general
fact that the square root of any non-square integer is irrational,
which is to say, incommensurable with the unit 1. It isn't clear
whether Theaetetus (or Plato) knew that two square roots such as
sqrt(2) and sqrt(3) are also incommensurable with each other, but
Karl Popper (in his anti-Plato polemic "The Free Society and its
Enemies") speculated that this might have been known, and that Plato's
choice of these two triangles as the basic components of his theory
was an attempt to provide a basis (in the mathematical sense) for
all possible numbers. In other words, Popper's idea is that Plato
tentatively thought the numbers 1, sqrt(2), and sqrt(3) are all
mutually incommensurable, but that it might be possible to construct
all other numbers, including sqrt(5), pi, etc., as rational functions
of these.
Of course, Book X of Euclid's Elements (cf. Prop 42) dashes this
hope, but it's possible that the propositions recorded there were
developed subsequent to Plato's time. Popper also makes much of the
numerical coincidence that sqrt(2)+sqrt(3) is approximately equal to
pi, and speculates that Plato might have thought these numbers were
exactly equal, but this doesn't seem credible to me. For one thing,
it would give a means of squaring the circle, which would certainly
have been mentioned if anyone had believed it. More importantly,
the basic insight of Theaetetus was in recognizing the symmetry of
all the infinitely many irrational square roots, and it just doesn't
seem likely that he (or Plato) would have been misled into supposing
that just two of them (along with the unit 1) could form the basis
for all the others. It's a very unnatural idea, one that would not
be likely to occur to a mathematician. (Still, an imaginative
interpreter could probably discern correspondences between the four
basis vectors of "The Platonic Field", i.e., numbers of the form
A+Bsqrt(2)+Csqrt(3)+Dsqrt(6), and Plato's four elements, not to
mention the components of Hamilton's quaternions.)
It's also interesting that Plato describes the "1,1,sqrt(2)" triangle
as the most "stable", and the most likely to hold its shape, thus
accounting for the inert and unchanging quality of the solid elements.
He didn't elaborate on his criterion for "stability", although we
can imagine that he had in mind the more nearly equal lengths of the
edges, being closer to equilibrium. On the other hand, this would
suggest that the equilateral triangle (which is the face of Plato's
"less stable" elements) was highly stable. Plato made no mention of
the fact that the cube is actually the only UNstable Platonic solid,
in the sense of rigidity of its edge structure. In addition, the
cube is the only Platonic solid that is NOT an equilibrium
configuration for its vertices on the surface of a sphere with
respect to an inverse-square repulsion. Nevertheless, the idea of
stability of the sub-atomic structure of solid is somewhat akin to
modern accounts of the stability of inert elements.
We can also discern echos of Plato's descriptions in Isaac Newton's
corpuscular theory. Newton's comments about the "sides" of light
particles are very reminiscent of Plato's language in Timaeus. It's
also interesting to compare some passages in Timaeus, such as
And so all these things were taken in hand, their natures
being determined by necessity in the way we've described,
by the craftsman of the most perfect and excellent among
things that come to be...
with phrases in Newton's Principia, such as
...All the diversity of created things, each in its place
and time, could only have arisen from the ideas and the
will of a necessarily existing being...
...all phenomena may depend on certain forces by which the
particles of bodies...either are impelled toward one another
and cohere in regular figures, or are repelled from one
another and recede...
...if anyone could work with perfect exactness, he would
be the most perfect mechanic of all...
Plato explicitly addressed the role of *necessity* in the design of
the universe (so well exemplified by the five and only five Platonic
solids), much as Einstein always said that what really interested
him was whether God had any choice in the creation of the world.
But Plato was not naive. He wrote
Although [God] did make use of the relevant auxiliary causes,
it was he himself who gave their fair design to all that comes
to be. That is why we must distinguish two forms of cause,
the divine and the necessary. First, the divine, for which we
must search in all things if we are to gain a life of happiness
to the extent that our nature allows, and second, the necessary,
for which we must search for the sake of the divine. Our reason
is that without the necessary, those other objects, about which
we are serious, cannot on their own be discerned, and hence
cannot be comprehended or partaken of in any other way.
The fifth element, i.e., the quintessence, according to Plato was
identified with the dodecahedron. He says simply "God used this
solid for the whole universe, embriodering figures on it". So, I
suppose it's a good thing that the right triangles comprising this
quintessence are incommensurate with those of the other four elements,
since we certainly wouldn't want the quintessence of the universe to
start transmuting into the baser subtances contained within itself!
Timaeus contains a very detailed discussion of virtually all aspects
of physical existence, including biology, cosmology, geography,
chemistry, physics, psychological perceptions, etc., all expressed in
terms of these four basic elements and their transmutations from one
into another by means of the constituient triangles being broken
apart and re-assembled into other forms. Overall it's a very
interesting and impressive theory, and strikingly similar in its
combinatorial (and numerological) aspects to some modern speculative
"theories of everything", as well as expressing ideas that have
obvious counterparts in the modern theory of chemistry and the
period table of elements, and so on.
Timaeus concludes
And so now we may say that our account of the universe has
reached its conclusion. This world of ours has received and
teems with living things, mortal and immortal. A visible
living thing containing visible things, and a perciptible
God, the image of the intelligible Living Thing. Its grandness,
goodness, beauty and perfection are unexcelled. Our one
universe, indeed, the only one of its kind, has come to be.
The speculative details of Plato's "account of the universe" are
not very satisfactory from the modern point of view, but there's
no doubt that - at least in its scope and ambition as an attempt
to represent "all that is" in terms of a small number of simple
mathematical operations - Plato's "theory of everything" left a
lasting impression on Western science.
Of course, it's not possible to build a pentagon from these two
basic kinds of right triangles, and Plato doesn't actually elaborate
on how the faces of the dodecahedron are to be constructed, but from
other sources we know that he thought each face should be comprosed
of 30 right triangles, probably as shown on the right-hand figure
above, so that the dodecahedron consisted of 360 triangles. The
tetrahedron, octahedron, and icosahedron consisted of 24, 48, and
120 triangles (of the type 1,2,sqrt(3)), respectively, and the
hexahedron consisted of 24 triangles (of the type 1,1,sqrt(2)).
Now, if the basic triangles were the subatomic particles, Plato
regarded the solids as the "atoms" or corpuscles of the various
forms of substance. In particular, he made the following
identifications
number of triangles
type 1 type 2
------ ------
tetrahedron = plasma ("fire") 24 0
octahedron = gas ("air") 48 0
icosahedron = liquid ("water") 120 0
hexahedron = solid ("earth") 0 24
The idea that all the constituients of nature consist of mixtures of a
small number of "elements", and in particular the selection of the four
elements of earth, water, air, and fire, is attributed to an earlier
Greek philosopher Empedocles of Agrigentum (495-435 BC). Empedocles
believed that although these elements (which he called "the roots of all
things") could be mixed together in various proportions, the elements
themselves were inviolable, and could never be changed. In contrast, one
of the intriguing aspects of Plato's theory was that he believed it was
possible for the subatomic particles to split up and re-combine into other
kinds of atoms. For example, he believed that a corpuscle of liquid,
consisting of 120 "type 1" triangles, could be broken up into five
corpuscles of plasma, or into two corpuscles of gas and and one of plasma.
Also, he believed that the "smaller" corpuscles could merge into larger
corpuscles, so that (for example) two atoms of plasma could merge and form
a single atom of gas. However, since the basic triangles making up "earth"
(cubes) are dis-similar to those of the other forms of substance, he held
that the triangles comprising cubes cannot be combined into any of the
other shapes. If a particle of earth happened to be broken up into its
constituient triangles, they will "drift about - whether the breaking
up within fire itself, or within a mass of air or water - until its
parts meet again somewhere, refit themselves together and become earth
again".
When Plato asserts that the [1,1,sqrt(2)] triangles cannot combine
into anything other than a cube, it's conceivable that he was basing
this on something more that just the geometric dis-similarity between
this triangle and the [1,2,sqrt(3)] triangle. He might also have
had in mind some notion of the incommensurability of the magnitudes
sqrt(2) and sqrt(3), not only with the unit 1, but with each other.
Indeed the same Theaetetus who gave the first complete account of the
five "Platonic" solids is also remembered for recognizing the general
fact that the square root of any non-square integer is irrational,
which is to say, incommensurable with the unit 1. It isn't clear
whether Theaetetus (or Plato) knew that two square roots such as
sqrt(2) and sqrt(3) are also incommensurable with each other, but
Karl Popper (in his anti-Plato polemic "The Free Society and its
Enemies") speculated that this might have been known, and that Plato's
choice of these two triangles as the basic components of his theory
was an attempt to provide a basis (in the mathematical sense) for
all possible numbers. In other words, Popper's idea is that Plato
tentatively thought the numbers 1, sqrt(2), and sqrt(3) are all
mutually incommensurable, but that it might be possible to construct
all other numbers, including sqrt(5), pi, etc., as rational functions
of these.
Of course, Book X of Euclid's Elements (cf. Prop 42) dashes this
hope, but it's possible that the propositions recorded there were
developed subsequent to Plato's time. Popper also makes much of the
numerical coincidence that sqrt(2)+sqrt(3) is approximately equal to
pi, and speculates that Plato might have thought these numbers were
exactly equal, but this doesn't seem credible to me. For one thing,
it would give a means of squaring the circle, which would certainly
have been mentioned if anyone had believed it. More importantly,
the basic insight of Theaetetus was in recognizing the symmetry of
all the infinitely many irrational square roots, and it just doesn't
seem likely that he (or Plato) would have been misled into supposing
that just two of them (along with the unit 1) could form the basis
for all the others. It's a very unnatural idea, one that would not
be likely to occur to a mathematician. (Still, an imaginative
interpreter could probably discern correspondences between the four
basis vectors of "The Platonic Field", i.e., numbers of the form
A+Bsqrt(2)+Csqrt(3)+Dsqrt(6), and Plato's four elements, not to
mention the components of Hamilton's quaternions.)
It's also interesting that Plato describes the "1,1,sqrt(2)" triangle
as the most "stable", and the most likely to hold its shape, thus
accounting for the inert and unchanging quality of the solid elements.
He didn't elaborate on his criterion for "stability", although we
can imagine that he had in mind the more nearly equal lengths of the
edges, being closer to equilibrium. On the other hand, this would
suggest that the equilateral triangle (which is the face of Plato's
"less stable" elements) was highly stable. Plato made no mention of
the fact that the cube is actually the only UNstable Platonic solid,
in the sense of rigidity of its edge structure. In addition, the
cube is the only Platonic solid that is NOT an equilibrium
configuration for its vertices on the surface of a sphere with
respect to an inverse-square repulsion. Nevertheless, the idea of
stability of the sub-atomic structure of solid is somewhat akin to
modern accounts of the stability of inert elements.
We can also discern echos of Plato's descriptions in Isaac Newton's
corpuscular theory. Newton's comments about the "sides" of light
particles are very reminiscent of Plato's language in Timaeus. It's
also interesting to compare some passages in Timaeus, such as
And so all these things were taken in hand, their natures
being determined by necessity in the way we've described,
by the craftsman of the most perfect and excellent among
things that come to be...
with phrases in Newton's Principia, such as
...All the diversity of created things, each in its place
and time, could only have arisen from the ideas and the
will of a necessarily existing being...
...all phenomena may depend on certain forces by which the
particles of bodies...either are impelled toward one another
and cohere in regular figures, or are repelled from one
another and recede...
...if anyone could work with perfect exactness, he would
be the most perfect mechanic of all...
Plato explicitly addressed the role of *necessity* in the design of
the universe (so well exemplified by the five and only five Platonic
solids), much as Einstein always said that what really interested
him was whether God had any choice in the creation of the world.
But Plato was not naive. He wrote
Although [God] did make use of the relevant auxiliary causes,
it was he himself who gave their fair design to all that comes
to be. That is why we must distinguish two forms of cause,
the divine and the necessary. First, the divine, for which we
must search in all things if we are to gain a life of happiness
to the extent that our nature allows, and second, the necessary,
for which we must search for the sake of the divine. Our reason
is that without the necessary, those other objects, about which
we are serious, cannot on their own be discerned, and hence
cannot be comprehended or partaken of in any other way.
The fifth element, i.e., the quintessence, according to Plato was
identified with the dodecahedron. He says simply "God used this
solid for the whole universe, embriodering figures on it". So, I
suppose it's a good thing that the right triangles comprising this
quintessence are incommensurate with those of the other four elements,
since we certainly wouldn't want the quintessence of the universe to
start transmuting into the baser subtances contained within itself!
Timaeus contains a very detailed discussion of virtually all aspects
of physical existence, including biology, cosmology, geography,
chemistry, physics, psychological perceptions, etc., all expressed in
terms of these four basic elements and their transmutations from one
into another by means of the constituient triangles being broken
apart and re-assembled into other forms. Overall it's a very
interesting and impressive theory, and strikingly similar in its
combinatorial (and numerological) aspects to some modern speculative
"theories of everything", as well as expressing ideas that have
obvious counterparts in the modern theory of chemistry and the
period table of elements, and so on.
Timaeus concludes
And so now we may say that our account of the universe has
reached its conclusion. This world of ours has received and
teems with living things, mortal and immortal. A visible
living thing containing visible things, and a perciptible
God, the image of the intelligible Living Thing. Its grandness,
goodness, beauty and perfection are unexcelled. Our one
universe, indeed, the only one of its kind, has come to be.
The speculative details of Plato's "account of the universe" are
not very satisfactory from the modern point of view, but there's
no doubt that - at least in its scope and ambition as an attempt
to represent "all that is" in terms of a small number of simple
mathematical operations - Plato's "theory of everything" left a
lasting impression on Western science.
Return to MathPages Main Menu
 On the other hand, if we make FOUR triangles maeet at a vertex, we
produce a square-bottomed pyramid, and we can obviously put two of
these together, base to base, to give a completely symmetrical
arrangement of eight triangular faces, called the octahedron, shown
below.
On the other hand, if we make FOUR triangles maeet at a vertex, we
produce a square-bottomed pyramid, and we can obviously put two of
these together, base to base, to give a completely symmetrical
arrangement of eight triangular faces, called the octahedron, shown
below.
 Next, we can make FIVE equilateral triangles meet at a point. It's
less obvious in this case, but if we continnue this pattern, adding
equilateral triangles so that five meet at each vertex, we arrive
as a complete solid with 20 triangular faces. This is called the
icosahedron, shown below.
Next, we can make FIVE equilateral triangles meet at a point. It's
less obvious in this case, but if we continnue this pattern, adding
equilateral triangles so that five meet at each vertex, we arrive
as a complete solid with 20 triangular faces. This is called the
icosahedron, shown below.
 Now, we might try putting SIX equilateral triangles together at a
point, but the result is a planar arrangement of triangles, so it
doesn't give a finite solid. I suppose we could regard this as
a Platonic solid with an infinite radius, which might have been
useful in Plato's cosmology, but it doesn't seem to have been viewed
this way. Perhaps this is not surprising, considering the well-known
aversion of the ancient Greek mathematicians to the complete infinity.
In any case, we clearly can't construct any more perfectly symmetrical
solids with equilateral triangle faces, so we must turn to other
possible face shapes.
The next regular polygon shape is the square, and again we find that
putting just two squares together does not yield a solid angle, so
we need at least three squares to meet at each vertex. Putting three
squares together we see that we can add three more to give the perfect
solid with six faces, called the hexahedron (also known as the cube).
This is shown below.
Now, we might try putting SIX equilateral triangles together at a
point, but the result is a planar arrangement of triangles, so it
doesn't give a finite solid. I suppose we could regard this as
a Platonic solid with an infinite radius, which might have been
useful in Plato's cosmology, but it doesn't seem to have been viewed
this way. Perhaps this is not surprising, considering the well-known
aversion of the ancient Greek mathematicians to the complete infinity.
In any case, we clearly can't construct any more perfectly symmetrical
solids with equilateral triangle faces, so we must turn to other
possible face shapes.
The next regular polygon shape is the square, and again we find that
putting just two squares together does not yield a solid angle, so
we need at least three squares to meet at each vertex. Putting three
squares together we see that we can add three more to give the perfect
solid with six faces, called the hexahedron (also known as the cube).
This is shown below.
 If we try to make FOUR square faces meet at each vertex, we have
another plane surface (giving another "infinite Platonic solid"), so
clearly this is the only finite perfectly symmetrical solid with
square faces.
Proceding to pentagonal (five-sided) faces, we find that if we put
together 12 pentagons so that three meet at each vertex, we arrive
at the fifth Platonic solid, called the dodecahedron, illustrated
below.
If we try to make FOUR square faces meet at each vertex, we have
another plane surface (giving another "infinite Platonic solid"), so
clearly this is the only finite perfectly symmetrical solid with
square faces.
Proceding to pentagonal (five-sided) faces, we find that if we put
together 12 pentagons so that three meet at each vertex, we arrive
at the fifth Platonic solid, called the dodecahedron, illustrated
below.
 It isn't self-evident that 12 identical regular pentagons would come
together perfectly like this to form a closed solid, but it works,
as Theaetetus proved and as Euclid demonstrates at the conclusion
of The Elements. Of course, if we accept that the icoshedron works,
then the dodecahedron automatically follows, because these two shapes
are "duals" of each other. This means that the icosahedron has 20
faces and 12 vertices, whereas the dodecahedron has 12 faces and 20
vertices, and the angular positions of the faces of one match up with
the positions of the vertices of the other. Thus, once we have the
icosahedron, we can just put a dot in the center of each face, connect
the dots, and viola!, we have a dodecahedron. Similarly, the cube
and the octahedron are duals of each other. Also, the tetrahedron is
the dual of itself (so to speak).
Clearly it's impossible for four (or more) pentagonal faces to meet at
a vertex, because they subtend more than 360 degrees. For hexagonal
(six-sided) faces, three hexagons meeting at a point constitute another
"infinite solid", i.e., so planar surface. It's also obvious that no
higher-order polygon can yield solid, so the five solids already
mentioned (tetrahedron, hexahedron, octahedron, icosahedron, and
dodecahedron) are the only regular polyhedrons.
Theaetetus not only proved that these solids exist, and that they are
the only perfectly symmetrical solids, he also gave the actual ratios
of the edge lengths E to the diameters D of the circumscribing spheres
for each of these solids. This is summarized in Propositions 13
through 17 of Euclid's Elements.
solid E/D
----------- --------------------
tetrahedron sqrt(2/3) 0.81649...
octahedron sqrt(1/2) 0.70710...
hexahedron sqrt(1/3) 0.57735...
icosahedron sqrt[(5-sqrt(5))/10] 0.52573...
dodecahedron [sqrt(5)-1]/[2sqrt(3)] 0.35682...
In Timaeus, Plato actually chose to constitute each of these solids
from right triangles, which played the role of the "sub-atomic
paticles" in his theory of everything. In turn, these trianglular
particles consisted of the three legs (which we might liken to quarks),
but these legs were ordinarily never separated. The right triangles
that he chose as his basis particles were of two types. One is
the "1,1,sqrt(2)" isoceles triangle formed by cutting a square in
half, and the the other is the "1,2,sqrt(3)" triangle formed by
cutting an equilateral triangle in half. He used these to construct
the faces of the first four solids, but oddly enough he didn't just
put two together, he used six "1,2,sqrt(3) triangles to make a
triangular face, and four "1,1,sqrt(2)" triangles to make a square
face, as shown below.
It isn't self-evident that 12 identical regular pentagons would come
together perfectly like this to form a closed solid, but it works,
as Theaetetus proved and as Euclid demonstrates at the conclusion
of The Elements. Of course, if we accept that the icoshedron works,
then the dodecahedron automatically follows, because these two shapes
are "duals" of each other. This means that the icosahedron has 20
faces and 12 vertices, whereas the dodecahedron has 12 faces and 20
vertices, and the angular positions of the faces of one match up with
the positions of the vertices of the other. Thus, once we have the
icosahedron, we can just put a dot in the center of each face, connect
the dots, and viola!, we have a dodecahedron. Similarly, the cube
and the octahedron are duals of each other. Also, the tetrahedron is
the dual of itself (so to speak).
Clearly it's impossible for four (or more) pentagonal faces to meet at
a vertex, because they subtend more than 360 degrees. For hexagonal
(six-sided) faces, three hexagons meeting at a point constitute another
"infinite solid", i.e., so planar surface. It's also obvious that no
higher-order polygon can yield solid, so the five solids already
mentioned (tetrahedron, hexahedron, octahedron, icosahedron, and
dodecahedron) are the only regular polyhedrons.
Theaetetus not only proved that these solids exist, and that they are
the only perfectly symmetrical solids, he also gave the actual ratios
of the edge lengths E to the diameters D of the circumscribing spheres
for each of these solids. This is summarized in Propositions 13
through 17 of Euclid's Elements.
solid E/D
----------- --------------------
tetrahedron sqrt(2/3) 0.81649...
octahedron sqrt(1/2) 0.70710...
hexahedron sqrt(1/3) 0.57735...
icosahedron sqrt[(5-sqrt(5))/10] 0.52573...
dodecahedron [sqrt(5)-1]/[2sqrt(3)] 0.35682...
In Timaeus, Plato actually chose to constitute each of these solids
from right triangles, which played the role of the "sub-atomic
paticles" in his theory of everything. In turn, these trianglular
particles consisted of the three legs (which we might liken to quarks),
but these legs were ordinarily never separated. The right triangles
that he chose as his basis particles were of two types. One is
the "1,1,sqrt(2)" isoceles triangle formed by cutting a square in
half, and the the other is the "1,2,sqrt(3)" triangle formed by
cutting an equilateral triangle in half. He used these to construct
the faces of the first four solids, but oddly enough he didn't just
put two together, he used six "1,2,sqrt(3) triangles to make a
triangular face, and four "1,1,sqrt(2)" triangles to make a square
face, as shown below.
 Of course, it's not possible to build a pentagon from these two
basic kinds of right triangles, and Plato doesn't actually elaborate
on how the faces of the dodecahedron are to be constructed, but from
other sources we know that he thought each face should be comprosed
of 30 right triangles, probably as shown on the right-hand figure
above, so that the dodecahedron consisted of 360 triangles. The
tetrahedron, octahedron, and icosahedron consisted of 24, 48, and
120 triangles (of the type 1,2,sqrt(3)), respectively, and the
hexahedron consisted of 24 triangles (of the type 1,1,sqrt(2)).
Now, if the basic triangles were the subatomic particles, Plato
regarded the solids as the "atoms" or corpuscles of the various
forms of substance. In particular, he made the following
identifications
number of triangles
type 1 type 2
------ ------
tetrahedron = plasma ("fire") 24 0
octahedron = gas ("air") 48 0
icosahedron = liquid ("water") 120 0
hexahedron = solid ("earth") 0 24
The idea that all the constituients of nature consist of mixtures of a
small number of "elements", and in particular the selection of the four
elements of earth, water, air, and fire, is attributed to an earlier
Greek philosopher Empedocles of Agrigentum (495-435 BC). Empedocles
believed that although these elements (which he called "the roots of all
things") could be mixed together in various proportions, the elements
themselves were inviolable, and could never be changed. In contrast, one
of the intriguing aspects of Plato's theory was that he believed it was
possible for the subatomic particles to split up and re-combine into other
kinds of atoms. For example, he believed that a corpuscle of liquid,
consisting of 120 "type 1" triangles, could be broken up into five
corpuscles of plasma, or into two corpuscles of gas and and one of plasma.
Also, he believed that the "smaller" corpuscles could merge into larger
corpuscles, so that (for example) two atoms of plasma could merge and form
a single atom of gas. However, since the basic triangles making up "earth"
(cubes) are dis-similar to those of the other forms of substance, he held
that the triangles comprising cubes cannot be combined into any of the
other shapes. If a particle of earth happened to be broken up into its
constituient triangles, they will "drift about - whether the breaking
up within fire itself, or within a mass of air or water - until its
parts meet again somewhere, refit themselves together and become earth
again".
When Plato asserts that the [1,1,sqrt(2)] triangles cannot combine
into anything other than a cube, it's conceivable that he was basing
this on something more that just the geometric dis-similarity between
this triangle and the [1,2,sqrt(3)] triangle. He might also have
had in mind some notion of the incommensurability of the magnitudes
sqrt(2) and sqrt(3), not only with the unit 1, but with each other.
Indeed the same Theaetetus who gave the first complete account of the
five "Platonic" solids is also remembered for recognizing the general
fact that the square root of any non-square integer is irrational,
which is to say, incommensurable with the unit 1. It isn't clear
whether Theaetetus (or Plato) knew that two square roots such as
sqrt(2) and sqrt(3) are also incommensurable with each other, but
Karl Popper (in his anti-Plato polemic "The Free Society and its
Enemies") speculated that this might have been known, and that Plato's
choice of these two triangles as the basic components of his theory
was an attempt to provide a basis (in the mathematical sense) for
all possible numbers. In other words, Popper's idea is that Plato
tentatively thought the numbers 1, sqrt(2), and sqrt(3) are all
mutually incommensurable, but that it might be possible to construct
all other numbers, including sqrt(5), pi, etc., as rational functions
of these.
Of course, Book X of Euclid's Elements (cf. Prop 42) dashes this
hope, but it's possible that the propositions recorded there were
developed subsequent to Plato's time. Popper also makes much of the
numerical coincidence that sqrt(2)+sqrt(3) is approximately equal to
pi, and speculates that Plato might have thought these numbers were
exactly equal, but this doesn't seem credible to me. For one thing,
it would give a means of squaring the circle, which would certainly
have been mentioned if anyone had believed it. More importantly,
the basic insight of Theaetetus was in recognizing the symmetry of
all the infinitely many irrational square roots, and it just doesn't
seem likely that he (or Plato) would have been misled into supposing
that just two of them (along with the unit 1) could form the basis
for all the others. It's a very unnatural idea, one that would not
be likely to occur to a mathematician. (Still, an imaginative
interpreter could probably discern correspondences between the four
basis vectors of "The Platonic Field", i.e., numbers of the form
A+Bsqrt(2)+Csqrt(3)+Dsqrt(6), and Plato's four elements, not to
mention the components of Hamilton's quaternions.)
It's also interesting that Plato describes the "1,1,sqrt(2)" triangle
as the most "stable", and the most likely to hold its shape, thus
accounting for the inert and unchanging quality of the solid elements.
He didn't elaborate on his criterion for "stability", although we
can imagine that he had in mind the more nearly equal lengths of the
edges, being closer to equilibrium. On the other hand, this would
suggest that the equilateral triangle (which is the face of Plato's
"less stable" elements) was highly stable. Plato made no mention of
the fact that the cube is actually the only UNstable Platonic solid,
in the sense of rigidity of its edge structure. In addition, the
cube is the only Platonic solid that is NOT an equilibrium
configuration for its vertices on the surface of a sphere with
respect to an inverse-square repulsion. Nevertheless, the idea of
stability of the sub-atomic structure of solid is somewhat akin to
modern accounts of the stability of inert elements.
We can also discern echos of Plato's descriptions in Isaac Newton's
corpuscular theory. Newton's comments about the "sides" of light
particles are very reminiscent of Plato's language in Timaeus. It's
also interesting to compare some passages in Timaeus, such as
And so all these things were taken in hand, their natures
being determined by necessity in the way we've described,
by the craftsman of the most perfect and excellent among
things that come to be...
with phrases in Newton's Principia, such as
...All the diversity of created things, each in its place
and time, could only have arisen from the ideas and the
will of a necessarily existing being...
...all phenomena may depend on certain forces by which the
particles of bodies...either are impelled toward one another
and cohere in regular figures, or are repelled from one
another and recede...
...if anyone could work with perfect exactness, he would
be the most perfect mechanic of all...
Plato explicitly addressed the role of *necessity* in the design of
the universe (so well exemplified by the five and only five Platonic
solids), much as Einstein always said that what really interested
him was whether God had any choice in the creation of the world.
But Plato was not naive. He wrote
Although [God] did make use of the relevant auxiliary causes,
it was he himself who gave their fair design to all that comes
to be. That is why we must distinguish two forms of cause,
the divine and the necessary. First, the divine, for which we
must search in all things if we are to gain a life of happiness
to the extent that our nature allows, and second, the necessary,
for which we must search for the sake of the divine. Our reason
is that without the necessary, those other objects, about which
we are serious, cannot on their own be discerned, and hence
cannot be comprehended or partaken of in any other way.
The fifth element, i.e., the quintessence, according to Plato was
identified with the dodecahedron. He says simply "God used this
solid for the whole universe, embriodering figures on it". So, I
suppose it's a good thing that the right triangles comprising this
quintessence are incommensurate with those of the other four elements,
since we certainly wouldn't want the quintessence of the universe to
start transmuting into the baser subtances contained within itself!
Timaeus contains a very detailed discussion of virtually all aspects
of physical existence, including biology, cosmology, geography,
chemistry, physics, psychological perceptions, etc., all expressed in
terms of these four basic elements and their transmutations from one
into another by means of the constituient triangles being broken
apart and re-assembled into other forms. Overall it's a very
interesting and impressive theory, and strikingly similar in its
combinatorial (and numerological) aspects to some modern speculative
"theories of everything", as well as expressing ideas that have
obvious counterparts in the modern theory of chemistry and the
period table of elements, and so on.
Timaeus concludes
And so now we may say that our account of the universe has
reached its conclusion. This world of ours has received and
teems with living things, mortal and immortal. A visible
living thing containing visible things, and a perciptible
God, the image of the intelligible Living Thing. Its grandness,
goodness, beauty and perfection are unexcelled. Our one
universe, indeed, the only one of its kind, has come to be.
The speculative details of Plato's "account of the universe" are
not very satisfactory from the modern point of view, but there's
no doubt that - at least in its scope and ambition as an attempt
to represent "all that is" in terms of a small number of simple
mathematical operations - Plato's "theory of everything" left a
lasting impression on Western science.
Of course, it's not possible to build a pentagon from these two
basic kinds of right triangles, and Plato doesn't actually elaborate
on how the faces of the dodecahedron are to be constructed, but from
other sources we know that he thought each face should be comprosed
of 30 right triangles, probably as shown on the right-hand figure
above, so that the dodecahedron consisted of 360 triangles. The
tetrahedron, octahedron, and icosahedron consisted of 24, 48, and
120 triangles (of the type 1,2,sqrt(3)), respectively, and the
hexahedron consisted of 24 triangles (of the type 1,1,sqrt(2)).
Now, if the basic triangles were the subatomic particles, Plato
regarded the solids as the "atoms" or corpuscles of the various
forms of substance. In particular, he made the following
identifications
number of triangles
type 1 type 2
------ ------
tetrahedron = plasma ("fire") 24 0
octahedron = gas ("air") 48 0
icosahedron = liquid ("water") 120 0
hexahedron = solid ("earth") 0 24
The idea that all the constituients of nature consist of mixtures of a
small number of "elements", and in particular the selection of the four
elements of earth, water, air, and fire, is attributed to an earlier
Greek philosopher Empedocles of Agrigentum (495-435 BC). Empedocles
believed that although these elements (which he called "the roots of all
things") could be mixed together in various proportions, the elements
themselves were inviolable, and could never be changed. In contrast, one
of the intriguing aspects of Plato's theory was that he believed it was
possible for the subatomic particles to split up and re-combine into other
kinds of atoms. For example, he believed that a corpuscle of liquid,
consisting of 120 "type 1" triangles, could be broken up into five
corpuscles of plasma, or into two corpuscles of gas and and one of plasma.
Also, he believed that the "smaller" corpuscles could merge into larger
corpuscles, so that (for example) two atoms of plasma could merge and form
a single atom of gas. However, since the basic triangles making up "earth"
(cubes) are dis-similar to those of the other forms of substance, he held
that the triangles comprising cubes cannot be combined into any of the
other shapes. If a particle of earth happened to be broken up into its
constituient triangles, they will "drift about - whether the breaking
up within fire itself, or within a mass of air or water - until its
parts meet again somewhere, refit themselves together and become earth
again".
When Plato asserts that the [1,1,sqrt(2)] triangles cannot combine
into anything other than a cube, it's conceivable that he was basing
this on something more that just the geometric dis-similarity between
this triangle and the [1,2,sqrt(3)] triangle. He might also have
had in mind some notion of the incommensurability of the magnitudes
sqrt(2) and sqrt(3), not only with the unit 1, but with each other.
Indeed the same Theaetetus who gave the first complete account of the
five "Platonic" solids is also remembered for recognizing the general
fact that the square root of any non-square integer is irrational,
which is to say, incommensurable with the unit 1. It isn't clear
whether Theaetetus (or Plato) knew that two square roots such as
sqrt(2) and sqrt(3) are also incommensurable with each other, but
Karl Popper (in his anti-Plato polemic "The Free Society and its
Enemies") speculated that this might have been known, and that Plato's
choice of these two triangles as the basic components of his theory
was an attempt to provide a basis (in the mathematical sense) for
all possible numbers. In other words, Popper's idea is that Plato
tentatively thought the numbers 1, sqrt(2), and sqrt(3) are all
mutually incommensurable, but that it might be possible to construct
all other numbers, including sqrt(5), pi, etc., as rational functions
of these.
Of course, Book X of Euclid's Elements (cf. Prop 42) dashes this
hope, but it's possible that the propositions recorded there were
developed subsequent to Plato's time. Popper also makes much of the
numerical coincidence that sqrt(2)+sqrt(3) is approximately equal to
pi, and speculates that Plato might have thought these numbers were
exactly equal, but this doesn't seem credible to me. For one thing,
it would give a means of squaring the circle, which would certainly
have been mentioned if anyone had believed it. More importantly,
the basic insight of Theaetetus was in recognizing the symmetry of
all the infinitely many irrational square roots, and it just doesn't
seem likely that he (or Plato) would have been misled into supposing
that just two of them (along with the unit 1) could form the basis
for all the others. It's a very unnatural idea, one that would not
be likely to occur to a mathematician. (Still, an imaginative
interpreter could probably discern correspondences between the four
basis vectors of "The Platonic Field", i.e., numbers of the form
A+Bsqrt(2)+Csqrt(3)+Dsqrt(6), and Plato's four elements, not to
mention the components of Hamilton's quaternions.)
It's also interesting that Plato describes the "1,1,sqrt(2)" triangle
as the most "stable", and the most likely to hold its shape, thus
accounting for the inert and unchanging quality of the solid elements.
He didn't elaborate on his criterion for "stability", although we
can imagine that he had in mind the more nearly equal lengths of the
edges, being closer to equilibrium. On the other hand, this would
suggest that the equilateral triangle (which is the face of Plato's
"less stable" elements) was highly stable. Plato made no mention of
the fact that the cube is actually the only UNstable Platonic solid,
in the sense of rigidity of its edge structure. In addition, the
cube is the only Platonic solid that is NOT an equilibrium
configuration for its vertices on the surface of a sphere with
respect to an inverse-square repulsion. Nevertheless, the idea of
stability of the sub-atomic structure of solid is somewhat akin to
modern accounts of the stability of inert elements.
We can also discern echos of Plato's descriptions in Isaac Newton's
corpuscular theory. Newton's comments about the "sides" of light
particles are very reminiscent of Plato's language in Timaeus. It's
also interesting to compare some passages in Timaeus, such as
And so all these things were taken in hand, their natures
being determined by necessity in the way we've described,
by the craftsman of the most perfect and excellent among
things that come to be...
with phrases in Newton's Principia, such as
...All the diversity of created things, each in its place
and time, could only have arisen from the ideas and the
will of a necessarily existing being...
...all phenomena may depend on certain forces by which the
particles of bodies...either are impelled toward one another
and cohere in regular figures, or are repelled from one
another and recede...
...if anyone could work with perfect exactness, he would
be the most perfect mechanic of all...
Plato explicitly addressed the role of *necessity* in the design of
the universe (so well exemplified by the five and only five Platonic
solids), much as Einstein always said that what really interested
him was whether God had any choice in the creation of the world.
But Plato was not naive. He wrote
Although [God] did make use of the relevant auxiliary causes,
it was he himself who gave their fair design to all that comes
to be. That is why we must distinguish two forms of cause,
the divine and the necessary. First, the divine, for which we
must search in all things if we are to gain a life of happiness
to the extent that our nature allows, and second, the necessary,
for which we must search for the sake of the divine. Our reason
is that without the necessary, those other objects, about which
we are serious, cannot on their own be discerned, and hence
cannot be comprehended or partaken of in any other way.
The fifth element, i.e., the quintessence, according to Plato was
identified with the dodecahedron. He says simply "God used this
solid for the whole universe, embriodering figures on it". So, I
suppose it's a good thing that the right triangles comprising this
quintessence are incommensurate with those of the other four elements,
since we certainly wouldn't want the quintessence of the universe to
start transmuting into the baser subtances contained within itself!
Timaeus contains a very detailed discussion of virtually all aspects
of physical existence, including biology, cosmology, geography,
chemistry, physics, psychological perceptions, etc., all expressed in
terms of these four basic elements and their transmutations from one
into another by means of the constituient triangles being broken
apart and re-assembled into other forms. Overall it's a very
interesting and impressive theory, and strikingly similar in its
combinatorial (and numerological) aspects to some modern speculative
"theories of everything", as well as expressing ideas that have
obvious counterparts in the modern theory of chemistry and the
period table of elements, and so on.
Timaeus concludes
And so now we may say that our account of the universe has
reached its conclusion. This world of ours has received and
teems with living things, mortal and immortal. A visible
living thing containing visible things, and a perciptible
God, the image of the intelligible Living Thing. Its grandness,
goodness, beauty and perfection are unexcelled. Our one
universe, indeed, the only one of its kind, has come to be.
The speculative details of Plato's "account of the universe" are
not very satisfactory from the modern point of view, but there's
no doubt that - at least in its scope and ambition as an attempt
to represent "all that is" in terms of a small number of simple
mathematical operations - Plato's "theory of everything" left a
lasting impression on Western science.